Boyle's Law
What is Boyle's Law?
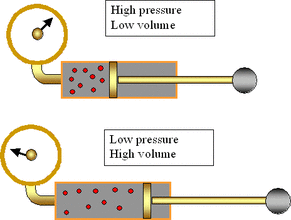
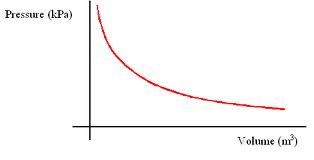
Boyle's Law states that at constant temperature, the pressure and volume of an ideal gas are inversely proportional. This can be represented mathematically by the equation PV = k. Plotting volume against pressure yields half a hyperbola
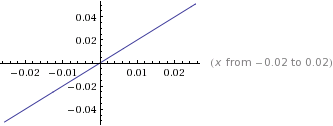
Consequently, a graph of 1 / V to P results in a straight line of slope k.
Boyle's Law can be used to calculate the volume or pressure of any ideal gas after the other variable has been changed, assuming constant temperature.
Thus Pinitial Vinitial = Pfinal Vfinal.
Example
5.0 L of CO2 gas is pumped into an evacuated rigid container at 1 atmosphere of pressure. The container was then put on a plane and flown to the peak of a mountain in the Swiss Alps where the pressure is only 0.34 atmospheres. What is the volume of the gas on top of the mountain? What will happen to the container?
By Boyle's Law, P1V1 = P2V2. Thus, (5.0 L)(1.0 atm) = (V2)(0.34 atm). V2 = 5.0 L x atm / 0.34 atm = 14.7 L.
At the top of mountain, the gas will occupy a volume of 14.7 L, causing the container to burst.
By Boyle's Law, P1V1 = P2V2. Thus, (5.0 L)(1.0 atm) = (V2)(0.34 atm). V2 = 5.0 L x atm / 0.34 atm = 14.7 L.
At the top of mountain, the gas will occupy a volume of 14.7 L, causing the container to burst.
Practice Problems
1. A 3.2 mL sample of gaseous 2 - vinylpyridine (C7H7N) is placed in an evacuated vault cylinder at 354 K and 2.3 kPa of pressure, and a piston is driven into the cylinder, reducing the volume of the cylinder to 2 mL. What is the final pressure of the 2 - vinylpyridine?
2. Given the graph below, calculate the constant of proportionality for Compound X and determine the volume occupied by the compound at 6.2 atmospheres of pressure.
2. Given the graph below, calculate the constant of proportionality for Compound X and determine the volume occupied by the compound at 6.2 atmospheres of pressure.
3. A gas was released into an unknown container. It was filled completely to the maximum capacity. The pressure of the container was measured and gave readings of 2.5 atm. The scientist believed too much gas was in the container, so he released some gas until the pressure reached 2.0 atm. What is the ratio of the new volume to the old volume?
4. Brian has a job pumping tires at the local gas station. Each tire can only withstand 5 atm of pressure before it explodes. Because he is used to pumping larger tires, Brian accidentally overpumps the tire, rupturing the tire. If the larger tires maintain a pressure of 3.4 atm and have a capacity of 4 L, how much air did Brian pump into the smaller tire?
4. Brian has a job pumping tires at the local gas station. Each tire can only withstand 5 atm of pressure before it explodes. Because he is used to pumping larger tires, Brian accidentally overpumps the tire, rupturing the tire. If the larger tires maintain a pressure of 3.4 atm and have a capacity of 4 L, how much air did Brian pump into the smaller tire?